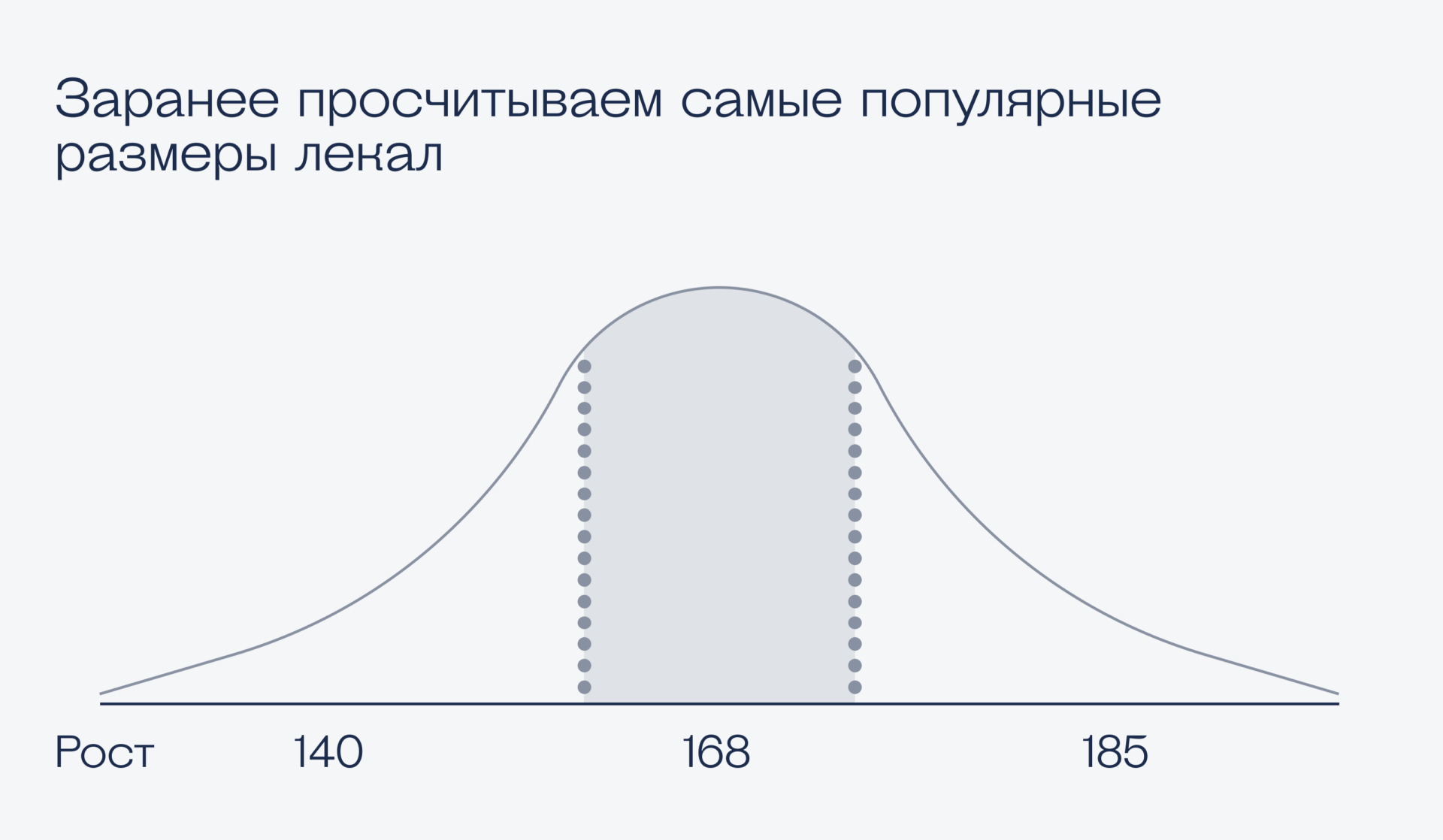
Гауссов закон распределения, или нормальное распределение, является одним из самых важных и широко применяемых статистических законов. Этот закон был впервые предложен Карлом Фридрихом Гауссом в начале XIX века, и с тех пор нашел множество применений в различных областях науки, экономике и технике.
Основная особенность гауссова закона распределения заключается в том, что он описывает симметричное и колоколообразное распределение случайной величины вокруг ее среднего значения. Форма этого распределения характеризуется двумя параметрами – средним значением и стандартным отклонением.
Гауссов закон распределения находит применение во множестве задач, где важно оценить вероятность того, что случайная величина попадет в определенный диапазон значений. Он широко используется в статистике для анализа данных, особенно в контексте проверки гипотез и построения доверительных интервалов.
Более того, гауссов закон распределения применяется в таких областях, как физика, финансы, биология, инженерия, информатика и многие другие. Он является ключевым инструментом для моделирования и прогнозирования различных процессов, а также для решения оптимизационных задач.
Гаусса закон распределения
Нормальное распределение имеет симметричную колоколообразную форму и характеризуется двумя параметрами: средним значением (математическим ожиданием) и стандартным отклонением. Вершина колокола соответствует среднему значению, а ширина колокола определяется стандартным отклонением.
Гаусса закон распределения является основой для многих статистических теорий и методов. Он широко применяется в области научных исследований, экономики, физики, социологии и других дисциплин для анализа данных, предсказания результатов и создания моделей.
Преимущество использования Гаусса закона распределения заключается в его математической простоте и универсальности. Он хорошо описывает большинство случайных переменных, которые возникают в естественных и социальных процессах, если их распределение близко к нормальному.
Важной особенностью нормального распределения является правило трех сигм, которое гласит, что около 68% данных находятся в пределах одного стандартного отклонения от среднего значения, около 95% данных — в пределах двух стандартных отклонений, и около 99.7% данных — в пределах трех стандартных отклонений. Это делает нормальное распределение особенно полезным для анализа и интерпретации данных.
Нормальное распределение также позволяет применять различные статистические тесты для проверки гипотез, оценки параметров и проведения прогнозов. Например, t-тест Стьюдента и анализ дисперсии основаны на предположении о нормальности данных.
Особенности Гаусса закона распределения
Гаусса закон распределения, также известный как нормальное распределение или распределение Гаусса-Лапласа, имеет несколько особенностей, которые делают его широко применимым в различных областях. Вот некоторые из этих особенностей:
- Симметричность: Гауссово распределение симметрично относительно своего среднего значения. Это означает, что вероятность значения, равного среднему, составляет наибольшую часть распределения.
- Центральная предельная теорема: Сумма большого количества независимых и одинаково распределенных случайных переменных, каждая из которых имеет конечное математическое ожидание и дисперсию, аппроксимируется нормальным распределением. Это означает, что Гауссово распределение является асимптотическим предельным распределением для многих других распределений.
- Мощный инструмент статистики: Гауссово распределение широко используется в статистике для моделирования и обработки данных. Его особенности, такие как центральная предельная теорема и свойства симметрии, делают его полезным для анализа различных видов данных.
- Устойчивость к выбросам: Гауссово распределение более устойчиво к выбросам, чем некоторые другие распределения. Это означает, что даже в присутствии некоторого количества выбросов, Гауссово распределение может по-прежнему давать хорошие результаты.
- Простота интерпретации: Гауссово распределение сравнительно просто в интерпретации. Математические параметры, такие как среднее значение и стандартное отклонение, имеют понятное смысловое значение, что erleichtert die Interpretation von Ergebnissen und Kommunikation mit anderen Fachleuten.
Все эти особенности делают Гауссово распределение мощным инструментом для моделирования и анализа данных в различных областях, включая статистику, физику, экономику, инженерию и многие другие.
Нормальное распределение
Нормальное распределение имеет форму колокола и симметрично относительно своего среднего значения. Среднее значение и стандартное отклонение определяют положение и форму графика нормального распределения. Большинство значений в нормальном распределении находятся вокруг среднего значения, а значения, находящиеся на краях, более редки.
Нормальное распределение имеет много применений в различных областях. Оно используется для описания случайных процессов в экономике, физике, биологии и других естественных и социальных науках. Например, в экономике нормальное распределение может быть использовано для описания распределения доходов или цен на товары. В физике оно может описывать случайные шумы и флуктуации в экспериментальных данных.
Одно из главных свойств нормального распределения — центральная предельная теорема. Согласно этой теореме, сумма большого числа независимых и одинаково распределенных случайных величин стремится к нормальному распределению, независимо от их исходных распределений. Это позволяет использовать нормальное распределение для приближенного описания различных случайных процессов.
Использование нормального распределения требует некоторых предположений о характере данных. Например, оно предполагает, что данные обладают симметричной формой распределения и малым числом выбросов. Если данные не удовлетворяют этим условиям, то другие распределения или методы статистического анализа могут быть более подходящими.
Симметричность и пик кривой
Симметричность кривой Гаусса позволяет использовать ее для моделирования и анализа многих естественных и социальных явлений, так как многие из них также характеризуются симметричным распределением значений.
Кроме того, кривая Гаусса имеет еще один важный особый пик — самый высокий уровень вероятности. Это означает, что наиболее вероятны будут значения, которые ближе к среднему значению. Чем дальше от него, тем меньше вероятность того, что случайная величина будет принимать такие значения.
Именно благодаря этому особому пику кривой Гаусса, она позволяет предсказывать вероятность того, что случайная величина будет принимать определенное значение. Это свойство делает распределение Гаусса важным инструментом в статистике и вероятностном моделировании.
| Значение | Вероятность |
|---|---|
| Среднее значение | Наибольшая |
| Близкое к среднему | Высокая |
| Далекое от среднего | Низкая |
Стандартное отклонение и куртозис
Куртозис — это мера остроты пика распределения и «тяжести» его хвостов. Он показывает, насколько вероятность выпадения значений около среднего значения отличается от вероятности выпадения значений в хвостах распределения. Куртозис может быть положительным или отрицательным: положительное значение означает более острую пиковую форму распределения и более тяжелые хвосты, отрицательное значение — более плоскую пиковую форму и более легкие хвосты.
Стандартное отклонение и куртозис являются важными характеристиками гауссового распределения, которые позволяют оценить его форму и разброс значений. Они используются в различных областях, таких как статистика, финансы, экономика, приборостроение и другие, для анализа данных, моделирования и прогнозирования.
Применение Гаусса закона распределения
Одно из основных применений Гаусса закона распределения — это моделирование случайных величин. Нормальное распределение хорошо подходит для моделирования физических, биологических, экономических и других процессов, которые подчиняются случайным флуктуациям.
Гауссовское распределение также используется для анализа и прогнозирования данных. Нормальное распределение позволяет оценить среднее значение и стандартное отклонение, что является важным для многих статистических методов. Кроме того, Гауссовское распределение используется при построении доверительных интервалов и тестировании гипотез.
Еще одним важным применением Гаусса закона распределения является аппроксимация других вероятностных распределений. Многие реальные процессы имеют сложную окраску и не могут быть точно описаны простыми вероятностными моделями. В таких случаях Гауссовское распределение может использоваться для приближенного описания этих процессов.
| Применение Гаусса закона распределения |
|---|
| Моделирование случайных величин |
| Анализ и прогнозирование данных |
| Аппроксимация других вероятностных распределений |
Финансовые анализы
Гауссово распределение, также известное как нормальное распределение, является одним из основных понятий в статистике и эконометрике. Оно используется для описания случайных переменных, которые имеют симметричное и сглаженное распределение значений. Такое распределение имеет много применений в финансовом анализе.
Одним из основных применений Гаусса закона распределения в финансовых анализах является прогнозирование финансовых показателей. По данным предыдущих периодов, можно построить модель распределения значений и использовать ее для предсказания будущих результатов. Это позволяет компаниям принимать обоснованные решения, основанные на предвидении возможных сценариев и рисков.
Кроме того, Гауссово распределение может использоваться для определения вероятности наступления определенных событий. Например, финансовый аналитик может использовать этот метод для оценки вероятности возникновения убытков или расчета доходности инвестиций. Это позволяет инвесторам и руководителям принимать осознанные решения, основанные на анализе рисков и прибыльности.
Вопрос-ответ:
Какой математический закон описывает распределение величин средних значений?
Для описания распределения средних значений применяется гауссовское (нормальное) распределение, или закон Гаусса.
Какие особенности имеет закон распределения Гаусса?
Закон распределения Гаусса имеет несколько особенностей. Во-первых, он симметричен относительно своего математического ожидания. Во-вторых, он имеет колоколообразную форму графика, с наибольшей вероятностью в окрестности математического ожидания. Также, он параметризуется двумя характеристиками: средним значением и стандартным отклонением.
Какое применение имеет закон распределения Гаусса?
Закон распределения Гаусса находит широкое применение в различных областях, связанных с анализом данных и моделированием. Например, он используется в статистике для описания случайной величины, в физике для описания шумовых процессов, в финансах для моделирования курсов валют и фондовых индексов, а также в машинном обучении и искусственном интеллекте для моделирования и прогнозирования данных.
Как возникает закон распределения Гаусса?
Закон распределения Гаусса возникает при соблюдении центральной предельной теоремы, которая утверждает, что сумма большого количество случайных независимых величин, имеющих любое распределение, будет приближаться к нормальному распределению с увеличением числа слагаемых.
Каковы основные свойства закона распределения Гаусса?
Основные свойства закона распределения Гаусса включают следующее: математическое ожидание и медиана совпадают и находятся в центре распределения, 50% значений находятся в интервале математического ожидания плюс-минус одно стандартное отклонение, 68% значений находятся в интервале математического ожидания плюс-минус два стандартных отклонения, и 95% значений находятся в интервале математического ожидания плюс-минус два стандартных отклонения.
Что такое закон распределения Гаусса?
Закон распределения Гаусса (или нормальное распределение) — это статистическое распределение, которое описывает случайные переменные во многих областях науки и инженерии. Оно характеризуется колоколообразной формой кривой, симметричной относительно среднего значения. Этот закон назван в честь Карла Фридриха Гаусса, немецкого математика и физика.





