Алгебра множеств – это раздел математики, в котором изучаются свойства и операции над множествами. Упрощение выражений с помощью законов и свойств алгебры множеств является одним из основных методов работы с множествами и позволяет сократить сложные выражения до более простой и понятной формы.
Законы и свойства алгебры множеств обладают определенными правилами, которые позволяют переставлять, удалять и объединять элементы в составе выражения. Например, закон коммутативности позволяет менять местами элементы внутри операции, а закон ассоциативности позволяет изменять порядок выполнения операций.
Упрощение выражения с помощью законов и свойств алгебры множеств является важным шагом при решении задач и упрощении сложных формул. Знание основных законов и свойств позволяет оптимизировать решение задачи и получить более четкое представление о структуре множества и его элементов.
В данной статье мы рассмотрим основные законы и свойства алгебры множеств, а также покажем, как они применяются для упрощения выражений. Кроме того, мы предоставим примеры и практические задачи, чтобы помочь вам лучше понять и освоить этот метод упрощения выражений.
Законы и свойства алгебры множеств
Одним из важных законов алгебры множеств является закон идемпотентности. Он утверждает, что объединение множества с самим собой не изменяет это множество: A ∪ A = A.
Другим важным законом алгебры множеств является закон коммутативности. Он утверждает, что порядок объединения или пересечения множеств не имеет значения: A ∪ B = B ∪ A и A ∩ B = B ∩ A.
Также существует закон ассоциативности, который гласит, что результат операции объединения или пересечения множеств не зависит от порядка выполнения операций: (A ∪ B) ∪ C = A ∪ (B ∪ C) и (A ∩ B) ∩ C = A ∩ (B ∩ C).
С помощью распределительного закона можно раскрыть скобки и упростить выражение: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) и A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Также существуют законы поглощения: A ∪ (A ∩ B) = A и A ∩ (A ∪ B) = A, а также законы де Моргана: (A ∪ B)’ = A’ ∩ B’ и (A ∩ B)’ = A’ ∪ B’.
Важно знать и применять эти законы и свойства при упрощении выражений и проведении операций с множествами.
Законы ассоциативности и коммутативности
Закон ассоциативности определяет, что результат операции над тремя элементами не зависит от скобочной структуры этих элементов. То есть, если у нас есть множество A, B и C, и мы выполняем операцию над ними, то результат будет одинаковым, независимо от того, в каком порядке мы выполняем операции.
| Выражение | Результат |
|---|---|
| (A ∪ B) ∪ C | A ∪ (B ∪ C) |
| (A ∩ B) ∩ C | A ∩ (B ∩ C) |
Закон коммутативности указывает на то, что порядок элементов в операции не играет роли для результата. Он позволяет менять местами элементы операции без изменения результата.
| Выражение | Результат |
|---|---|
| A ∪ B | B ∪ A |
| A ∩ B | B ∩ A |
Законы ассоциативности и коммутативности широко применяются в математике и информатике для упрощения выражений, улучшения производительности и оптимизации алгоритмов. Они также являются основой для дальнейших знаний и исследований в алгебре множеств.
Закон ассоциативности
Суть закона ассоциативности заключается в том, что при выполнении операции над тремя множествами, порядок выполнения операций между ними не влияет на конечный результат. То есть, для любых множеств A, B и C, справедливо следующее равенство:
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
- (A ∩ B) ∩ C = A ∩ (B ∩ C)
Этот закон можно иллюстрировать на примере объединения и пересечения множеств. Например, пусть у нас есть множества:
- A = {1, 2}
- B = {2, 3}
- C = {3, 4}
Тогда применение закона ассоциативности позволит нам переставить скобки и получить одинаковый результат:
- (A ∪ B) ∪ C = ({1, 2} ∪ {2, 3}) ∪ {3, 4} = {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
- A ∪ (B ∪ C) = {1, 2} ∪ ({2, 3} ∪ {3, 4}) = {1, 2} ∪ {2, 3, 4} = {1, 2, 3, 4}
Таким образом, мы видим, что порядок выполнения операций не влияет на конечный результат, а значит, мы можем упростить выражения, используя закон ассоциативности.
Закон коммутативности
В случае объединения множеств, а именно операции «объединение», закон коммутативности можно выразить следующим образом:
- Ассоциативность: A ∪ (B ∪ C) = (A ∪ B) ∪ C
- Коммутативность: A ∪ B = B ∪ A
То есть, для любых множеств A, B и C выполняются данные условия. Другими словами, порядок множеств, которые объединяются, не важен.
Закон коммутативности также применим к операции пересечения множеств. В этом случае он формулируется следующим образом:
- Ассоциативность: A ∩ (B ∩ C) = (A ∩ B) ∩ C
- Коммутативность: A ∩ B = B ∩ A
То есть, для любых множеств A, B и C выполняются данные условия. Операция пересечения также не зависит от порядка множеств, которые пересекаются.
Закон коммутативности является важным инструментом при упрощении выражений с помощью законов и свойств алгебры множеств. Он позволяет менять порядок элементов и упрощать выражения без изменения результата.
Законы дистрибутивности
Первый закон дистрибутивности, известный как закон дистрибутивности умножения относительно сложения, позволяет раскрыть скобки и перегруппировать слагаемые:
| (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) | (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) |
Второй закон дистрибутивности, известный как закон дистрибутивности сложения относительно умножения, позволяет раскрыть скобки и перегруппировать множители:
| (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) | (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) |
Третий закон дистрибутивности, известный как общий дистрибутивный закон, позволяет раскрыть скобки в выражении, состоящем из двух операций:
| A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
Знание и применение законов дистрибутивности значительно упрощает решение задач и упрощение выражений в алгебре множеств.
Закон дистрибутивности пересечения относительно объединения
Согласно закону дистрибутивности пересечение множества A с объединением множеств B и C равно объединению пересечений множеств A с B и A с C. Формально этот закон записывается следующим образом:
(A ∩ (B ∪ C)) = ((A ∩ B) ∪ (A ∩ C))
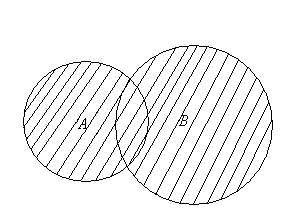
Наглядно этот закон можно представить с помощью диаграммы Венна:
- Слева: Множество A пересекается с объединением множеств B и C.
- Справа: Множество A пересекается с множеством B, а затем с множеством C, а результат объединяется.
Применение закона дистрибутивности пересечения относительно объединения позволяет упростить выражения и упростить работу с множествами в алгебре множеств.
Закон дистрибутивности объединения относительно пересечения
В алгебре множеств существует закон дистрибутивности объединения относительно пересечения. Этот закон позволяет упрощать выражения, содержащие операции объединения и пересечения множеств.
Закон дистрибутивности объединения относительно пересечения формулируется следующим образом:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
где A, B и C — произвольные множества.
Интуитивно, закон можно понимать так: если мы объединяем множество A с результатом пересечения множеств B и C, то это эквивалентно объединению множеств A и B, а затем объединению множеств A и C. То есть порядок выполняемых операций не важен.
Закон дистрибутивности объединения относительно пересечения может быть полезен при упрощении выражений с множествами. Он позволяет сокращать количество операций и упрощать формулы для более удобного представления данных.
Пример применения закона дистрибутивности объединения относительно пересечения:
Пусть A = {1, 2, 3}, B = {2, 3, 4} и C = {3, 4, 5}. Тогда:
- A ∪ (B ∩ C) = A ∪ {3} = {1, 2, 3}
- (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4} ∩ {1, 2, 3, 4, 5} = {1, 2, 3, 4}
Можно видеть, что результаты выражений совпадают, что подтверждает корректность закона дистрибутивности объединения относительно пересечения.
Вопрос-ответ:
Можно ли упростить выражение, используя только одно свойство алгебры множеств?
Да, в некоторых случаях выражение можно упростить, используя только одно свойство алгебры множеств. Например, если используется закон дополнения, то исходное множество можно заменить на универсальное множество или пустое множество, в зависимости от наличия отрицания. Однако в большинстве случаев для полного упрощения выражения требуется использование нескольких законов и свойств алгебры множеств.
Какие законы алгебры множеств помогут упростить выражение?
Существует несколько законов алгебры множеств, которые помогут упростить выражение. Некоторые из них включают коммутативный, ассоциативный и дистрибутивный законы, а также законы дополнения и идемпотентности.
Как применить коммутативный закон алгебры множеств?
Коммутативный закон алгебры множеств утверждает, что порядок объединения или пересечения множеств не имеет значения. Таким образом, если у вас есть выражение A ∪ B, вы можете поменять местами множества и записать его как B ∪ A. То же самое относится и к операции пересечения: A ∩ B эквивалентно B ∩ A.