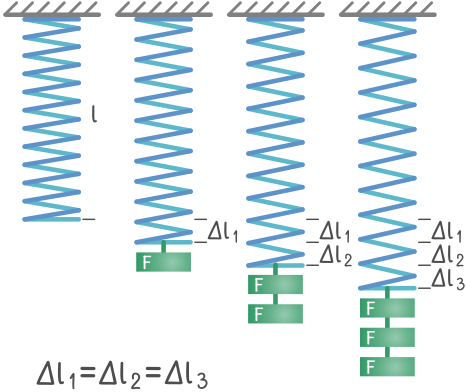
Закон Гука является одной из фундаментальных концепций в области механики и отражает взаимосвязь между деформацией тела и силой, действующей на него. Этот закон назван в честь английского физика Роберта Гука, который впервые сформулировал его в XVII веке.

Основное утверждение Закона Гука состоит в том, что деформация тела пропорциональна силе, вызывающей эту деформацию. Более конкретно, изменение длины тела прямо пропорционально приложенной силе и обратно пропорционально площади поперечного сечения тела.

Формула Закона Гука имеет вид F = k * Δl, где F — сила, k — коэффициент упругости, Δl — изменение длины тела. Коэффициент упругости (некоторыми обозначается как Е) определяет жесткость материала и является постоянной для данного материала при определенных условиях.

Важно отметить, что Закон Гука работает только при малых деформациях, когда материал возвращается в исходное состояние после прекращения действия силы. Если деформация становится слишком велика, то материал может испытать пластическую деформацию или разрушение.

Что такое Закон Гука

Согласно Закону Гука, деформация твердого тела пропорциональна силе, вызывающей эту деформацию. Если на тело действует сила вдоль его оси, то формула Закона Гука имеет вид:

F = k * Δl

где:

F — сила, вызывающая деформацию

k — коэффициент упругости (жесткость) материала

Δl — изменение длины тела под воздействием силы F

Коэффициент упругости определяет степень жесткости материала и связан с его упругими свойствами. Чем больше коэффициент упругости, тем сильнее будет возникать деформация при заданной силе.

Закон Гука позволяет рассчитать деформацию материала и понять, как он будет вести себя при различных силах. Этот закон широко применяется в инженерных расчетах, механике, строительстве и других отраслях, связанных с изучением деформаций твердых тел.

Определение и история

Этот закон был открыт и сформулирован в 17 веке робототехником и физиком Робертом Гуком. Роберт Гук провел множество экспериментов с растяжимыми телами и заметил, что сила, действующая на растягиваемый предмет, пропорциональна величине его деформации.

Впервые закон Гука был опубликован в книге «De Potentia Restitutiva», которая вышла в 1678 году. В этой работе Гук формулирует закон и проводит серию экспериментов для его подтверждения.

Закон Гука имеет широкое применение в инженерии, физике и других областях науки. Он позволяет рассчитывать деформацию твердых тел при действии силы и проводить ряд других технических расчетов.

Формула Закона Гука

Формула Закона Гука имеет вид:

F = k * Δl

где:

• F — сила, действующая на материал.
• k — коэффициент упругости (также называемый модулем упругости).
• Δl — изменение длины материала.

Эта формула показывает, что сила, действующая на материал, пропорциональна его изменению длины. Коэффициент упругости определяет, насколько сильно будет деформироваться материал при действии силы.

Формула Закона Гука также может быть переписана в других формах, например:

• Δl = F / k — формула для расчета изменения длины материала при известной силе и коэффициенте упругости.
• k = F / Δl — формула для расчета коэффициента упругости при известной силе и изменении длины материала.

Формула Закона Гука является основой для решения множества задач в области физики и инженерии. Она позволяет предсказывать деформации материалов и рассчитывать необходимые параметры для конструирования упругих систем.

Примеры расчета по Закону Гука

F = k * Δl

где F — сила, k — коэффициент упругости, Δl — изменение длины.

Рассмотрим пример для наглядности. Пусть у нас есть пружина с коэффициентом упругости k равным 100 Н/м и длиной 1 м. Если мы применяем к этой пружине силу 10 Н, то согласно Закону Гука мы можем расчитать изменение длины пружины:

F = k * Δl

10 Н = 100 Н/м * Δl

Отсюда получаем:

Δl = 10 Н / (100 Н/м)

Δl = 0,1 м или 10 см

Таким образом, применение силы 10 Н к пружине с коэффициентом упругости 100 Н/м приведет к увеличению длины пружины на 0,1 м или 10 см.

Второй пример. Пусть у нас есть стальная проволока с коэффициентом упругости k равным 200 Н/мм и длиной 50 мм. Если мы применяем к этой проволоке силу 20 Н, то рассчитаем изменение длины проволоки:

F = k * Δl

20 Н = 200 Н/мм * Δl

Отсюда получаем:

Δl = 20 Н / (200 Н/мм)

Δl = 0,1 мм

Таким образом, применение силы 20 Н к стальной проволоке с коэффициентом упругости 200 Н/мм приведет к увеличению длины проволоки на 0,1 мм.

Это лишь два примера расчета по Закону Гука, но принцип и формула остаются одинаковыми для всех упругих материалов.

Пример 1: Растяжение пружины

Для наглядного объяснения закона Гука рассмотрим пример с растяжением пружины. Пусть задана пружина с коэффициентом жесткости k=1000 Н/м (ньютон на метр), которую растягивают с силой F=500 Н (ньютон). Найдем изменение длины пружины.

Из закона Гука:

F = k * x

где F — сила, k — коэффициент жесткости пружины, x — изменение длины пружины.

Подставляя известные значения, получим:

500 = 1000 * x

Отсюда найдем изменение длины пружины:

x = 500 / 1000

x = 0.5 м (метра)

Таким образом, при растяжении пружины с силой 500 Нейтонов, ее длина изменится на 0.5 метра.

Пример 2: Сжатие пружины

Допустим, у нас есть пружина с жесткостью к = 100 Н/м. Мы применяем силу F = 50 Н к пружине, сжимая ее на расстояние х = 0,2 м. Какое усилие будет действовать в пружине?

1. Найдем коэффициент упругости пружины:
• Коэффициент упругости пружины определяется соотношением: к = F / х;
• Подставляем известные значения: 100 = F / 0,2;
• Решаем уравнение: F = 100 * 0,2 = 20 Н.
2. Таким образом, усилие, действующее в пружине при сжатии на 0,2 м будет равно 20 Н.

Этот пример демонстрирует, как применение силы к пружине может вызвать сжатие пружины и действие обратной силы, называемой усилием пружины. Результаты расчетов позволяют предсказать поведение пружины при возникновении определенной силы и сжатии.

Вопрос-ответ:

Что такое закон Гука?

Закон Гука — это физический закон, описывающий связь между силой, действующей на упругое тело, и его деформацией. Согласно закону Гука, деформация прямо пропорциональна силе действующей на тело.

Какова формула закона Гука?

Формула закона Гука выглядит следующим образом: F = k * Δl, где F — сила, действующая на тело; k — коэффициент пропорциональности (также называемый коэффициентом упругости); Δl — изменение длины тела.

Как рассчитать коэффициент упругости по формуле закона Гука?

Для расчета коэффициента упругости (k) по формуле закона Гука необходимо измерить силу (F), действующую на тело, и изменение длины (Δl) этого тела под действием силы. После получения этих данных, коэффициент упругости можно рассчитать как отношение силы к изменению длины.

Какие единицы измерения используются при работе с законом Гука?

Единицы измерения, используемые при работе с законом Гука, зависят от конкретных величин, с которыми мы работаем. Например, сила может быть измерена в ньютонах (Н), длина — в метрах (м), а коэффициент упругости — в паскалях (Па).

Какие существуют примеры расчета, основанные на законе Гука?

Примеры расчета, основанные на законе Гука, включают определение силы, действующей на упругое тело при известном изменении его длины и известном коэффициенте упругости, а также определение изменения длины тела при известной силе и известном коэффициенте упругости. В этих расчетах используется формула закона Гука — F = k * Δl.