Закон Кеплера третий – это одна из ключевых формулировок, описывающих движение планет вокруг Солнца. Данный закон говорит нам о зависимости периода обращения планеты вокруг Солнца от её среднего расстояния до него. Уже в XVII веке Иоганн Кеплер продемонстрировал эту закономерность исследуя планетарные данные, и его труды принесли революцию в наши представления о небесных телах.
Закон Кеплера третий формулируется следующим образом: квадрат периода обращения планеты (время, которое планета требует для совершения полного оборота вокруг Солнца) пропорционален кубу среднего расстояния планеты до Солнца. То есть, математически закон Кеплера третий выражается как T^2 = k * R^3, где T – период обращения планеты, R – среднее расстояние от планеты до Солнца, а k – постоянная.
Применение закона Кеплера третьего позволяет нам установить взаимосвязь между периодом обращения планеты и её средним расстоянием до Солнца. Благодаря этому закону мы можем прогнозировать, какой период обращения у планеты и насколько далеко она находится от своей звезды. Также закон Кеплера третий обеспечивает основу для установления закономерностей в движении всех небесных тел и помогает нам лучше понять строение Вселенной.
Определение третьего закона Кеплера
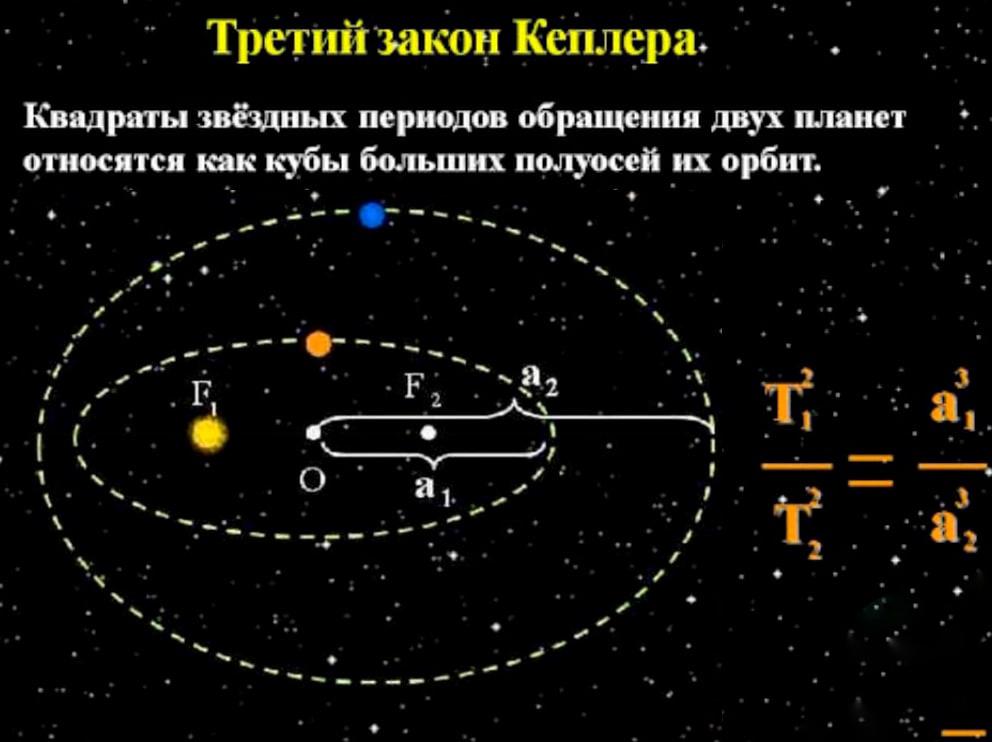
Третий закон Кеплера, также известный как закон периодов или гармонический закон, формулирует математическую связь между периодами обращения планет вокруг Солнца и их средними расстояниями до Солнца. Согласно данному закону, квадраты периодов обращения двух планет пропорциональны кубам их средних расстояний до Солнца.
То есть, если T1 и T2 — периоды обращения двух планет, а R1 и R2 — средние расстояния этих планет до Солнца, то выполняется следующая формула:
T12/T22 = R13/R23
Этот закон позволяет определить период обращения планеты вокруг Солнца, зная её среднее расстояние до Солнца, либо определить среднее расстояние, зная период обращения.
Третий закон Кеплера был сформулирован немецким астрономом Иоганном Кеплером в XVII веке. Он опирался на наблюдения Тихо Браге и Зоарта Байера, а также на свои собственные собственные исследования.
Формула закона Кеплера
Закон Кеплера выражает математическую связь между периодом обращения планеты вокруг Солнца и радиусом ее орбиты. Третий закон Кеплера можно записать в виде следующей формулы:
| Закон Кеплера |
|---|
| Период обращения (T) в квадрате пропорционален кубу большой полуоси (a) орбиты: |
| T2 = k * a3 |
Здесь T обозначает период обращения планеты (время, за которое она совершает полный оборот вокруг Солнца), a — большую полуось орбиты (расстояние от планеты до Солнца), а k — постоянную пропорциональности.
Третий закон Кеплера является одним из фундаментальных законов в астрономии и подтверждает тесную связь между движением планет и их расстоянием от Солнца. Формула закона Кеплера позволяет предсказывать и исследовать движение планет и других небесных тел в Солнечной системе.
Взаимосвязь с другими законами
Первый закон Кеплера, также известный как закон орбит, утверждает, что планеты движутся по эллиптическим орбитам, где Солнце находится в одном из фокусов. Этот закон подтверждает, что орбиты планет являются закрытыми эллипсами, а не окружностями.
Второй закон Кеплера, также называемый законами равных площадей, утверждает, что радиус-вектор, проведенный из Солнца к планете, за равные промежутки времени описывает равные площади. То есть, планета приближается к Солнцу и отдаляется от него с разной скоростью, но путь, пройденный по орбите, равномерно заполняет площадь.
Второй закон Кеплера является основой для формулировки третьего закона. Это связано с тем, что период обращения планеты вокруг Солнца зависит от длины большой полуоси её орбиты и средней скорости планеты в ней. Чем больше полуось орбиты, тем дольше длится период обращения планеты.
Третий закон Кеплера может быть выражен математически с использованием формулы T² = k × a³. Здесь T — период обращения планеты вокруг Солнца, a — длина большой полуоси орбиты планеты, а k — некоторая константа.
Таким образом, взаимосвязь между третьим законом Кеплера и двумя предыдущими законами заключается в том, что третий закон вытекает из законов орбит и равных площадей. Он дополняет предыдущие законы, предоставляя математическую модель, описывающую соотношение между периодом обращения планеты и длиной её орбиты.
Применение третьего закона Кеплера
Третий закон Кеплера, также известный как закон гармоничных интервалов, имеет важное применение в астрономии и космических исследованиях. Этот закон позволяет определить отношение периодов обращения планет вокруг Солнца или других тел в Солнечной системе.
Согласно закону Кеплера, квадрат периода обращения планеты пропорционален кубу большой полуоси ее орбиты. Это означает, что периодическое движение планет вокруг Солнца может быть описано математической формулой:
T^2 = k * a^3
где T — период обращения планеты (время, необходимое для одного оборота), a — большая полуось орбиты планеты, а k — постоянная, зависящая от массы и положения тел.
Таким образом, применение третьего закона Кеплера позволяет установить связь между периодом обращения планеты и ее орбитальными параметрами. Это позволяет астрономам предсказывать движение планет и предоставлять информацию о времени, необходимом для прохождения определенного пути вокруг Солнца.
Закон Кеплера также является основой для изучения и классификации других систем планет и звезд. Используя этот закон, ученые могут определить структуру и свойства других солнечных систем, что помогает расширить наши знания о Вселенной.
Применение третьего закона Кеплера также находит применение в различных инженерных и технических областях. Например, в космической навигации и синхронизации спутников, где расчеты основанные на законе Кеплера позволяют точно определить положение и время перелета искусственных спутников. Также, этот закон используется в аэрокосмической инженерии для расчета орбитальных параметров при запуске космических аппаратов.
Использование в астрономии
В астрономии этот закон играет важную роль при изучении различных астрономических объектов. Например, с его помощью можно вычислить период обращения планеты вокруг Солнца или спутника вокруг планеты. Это позволяет установить множество интересных фактов о небесных телах и их характеристиках.
Кроме того, закон Кеплера третий помогает астрономам в поиске новых планет и спутников внутри и за пределами Солнечной системы. Используя этот закон, можно вычислить период обращения планеты и предсказать ее наличие в определенном области неба.
Также, закон Кеплера третий применяется для изучения двойных звезд и их орбитальных характеристик. Астрономы используют этот закон для определения периода обращения двойной звезды и ее физических параметров.
Таким образом, использование закона Кеплера третьего в астрономии позволяет получать ценную информацию о движении планет и спутников, исследовать астрономические объекты и находить новые планеты и спутники.
Практическое применение
Закон Кеплера третий играет важную роль в навигации и космических исследованиях. Он позволяет определить положение и движение планет и спутников вокруг своих звездных систем.
Одним из примеров практического применения закона Кеплера третьего является использование его формулы для расчета орбитального периода и расстояния для спутников искусственных спутников Земли. По формуле можно определить период обращения искусственного спутника Земли вокруг планеты при известном расстоянии от центра Земли до спутника.
Другое применение закона Кеплера третьего заключается в изучении планетарных систем вне Солнечной системы. С помощью формулы закона Кеплера третьего можно определить орбитальные элементы и характеристики планетарных систем на основе наблюдаемых данных. Это помогает ученым лучше понять и классифицировать различные типы планетарных систем в галактике.
Кроме того, закон Кеплера третий используется в астрономических калькуляторах и программных средствах для проведения астрономических расчетов и прогнозирования орбитальных и астрономических событий. Он дает возможность предсказать положение планет и других небесных объектов в определенное время, что имеет важное значение для практического использования в обзорных и наблюдательных астрономических исследованиях.
Таким образом, практическое применение закона Кеплера третьего включает навигацию, космические исследования, изучение планетарных систем и использование в астрономических расчетах и прогнозах. Этот закон является основополагающим для понимания динамики движения небесных тел во Вселенной и играет ключевую роль в различных астрономических дисциплинах и приложениях.
Особенности третьего закона Кеплера
Третий закон Кеплера, также известный как закон периодов, гласит, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам их больших полуосей.
Особенностью этого закона является то, что он относится не только к планетам, но и к любым другим небесным телам — спутникам, астероидам и кометам. Это делает его универсальным законом для всего движения небесных объектов.
Еще одной особенностью закона периодов является то, что он позволяет определить относительные расстояния между планетами. Например, если известен период обращения одной планеты и ее большая полуось, можно вычислить периоды обращения других планет и их расстояния до Солнца.
Закон Кеплера используется для расчета множества космических миссий. Например, при планировании миссий к другим планетам важно знать периоды их обращения, чтобы определить наиболее подходящее время для запуска и встречи с этими планетами.
Таким образом, особенности третьего закона Кеплера делают его важным инструментом для изучения и понимания движения небесных тел.
Объяснение движения планет
Движение планет вокруг Солнца объясняется с помощью Закона Кеплера. Закон Кеплера третий утверждает, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси ее орбиты.
Период обращения планеты вокруг Солнца — это время, за которое планета совершает полный оборот вокруг Солнца. Большая полуось орбиты является половиной наибольшего расстояния между планетой и Солнцем.
Формула Закона Кеплера третьего:
T^2 = k * a^3
где T — период обращения планеты вокруг Солнца, a — большая полуось орбиты планеты, k — постоянная для каждой планеты и Солнца.
Закон Кеплера третий позволяет точно определить период обращения и расстояние между планетами и Солнцем. Он также позволяет предсказывать, как долго займет у планеты совершить полный оборот.
Кроме того, Закон Кеплера третий является одним из ключевых компонентов общей теории гравитации, сформулированной Ньютоном. Он позволяет понять, как взаимодействие гравитационной силы между планетой и Солнцем определяет их движение и форму орбиты.
Универсальность закона
Однако, следует отметить, что закон Кеплера третий не ограничивается только планетарными системами. Он также применим к другим небесным объектам, таким как спутники, кометы и астероиды. Даже движение искусственных спутников Земли также может быть описано этим законом.
Универсальность закона Кеплера третьего заключается в том, что он применим к различным объектам и системам, что делает его важным инструментом для изучения движения и взаимодействия небесных тел. Формула закона Кеплера третьего демонстрирует простоту и эффективность для описания такого сложного явления, как орбитальное движение.
Применение закона Кеплера третьего позволяет ученым проводить детальные исследования и расчеты орбитальных характеристик планет, спутников и других небесных объектов. Это важное средство для предсказания, моделирования и изучения космических явлений и процессов.
| Применение закона Кеплера третьего | Объекты и системы |
|---|---|
| Наблюдение планетарных систем | Планеты вокруг Солнца |
| Изучение спутников | Луна вокруг Земли, спутники планет |
| Анализ движения комет и астероидов | Небесные тела в Солнечной системе |
| Моделирование орбитального движения искусственных спутников Земли | Искусственные спутники Земли |
Таким образом, закон Кеплера третий является всеобъемлющим и применимым законом, который позволяет ученым исследовать и понимать множество небесных объектов и систем, а также предсказывать и моделировать их движение и взаимодействие с высокой точностью.
Вопрос-ответ:
Как формулируется закон Кеплера третий?
Закон Кеплера третий утверждает, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу большей полуоси ее орбиты.
В чем заключается основная особенность третьего закона Кеплера?
Основной особенностью третьего закона Кеплера является то, что он устанавливает связь между периодом обращения планеты и размерами ее орбиты.
Как можно применить третий закон Кеплера в практических расчетах?
Третий закон Кеплера может быть использован для определения периода обращения планеты вокруг Солнца на основе известных размеров орбиты или наоборот — для определения размеров орбиты, основываясь на известном периоде обращения.
Какие еще законы Кеплера необходимо учитывать при использовании третьего закона?
При использовании третьего закона Кеплера необходимо также учесть первый и второй законы, которые описывают форму и скорость движения планеты во время обращения вокруг Солнца.
Можно ли применять третий закон Кеплера для других небесных объектов, кроме планет?
Да, третий закон Кеплера может быть применен не только для планет, но и для других небесных объектов, таких как спутники, астероиды и кометы.
Как формулируется закон Кеплера третий?
Закон Кеплера третий формулируется следующим образом: квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси орбиты.
Какая формула описывает закон Кеплера третий?
Формула Кеплера третьего закона выглядит так: T^2 = k * a^3, где T — период обращения планеты вокруг Солнца, a — большая полуось орбиты, k — постоянный коэффициент.